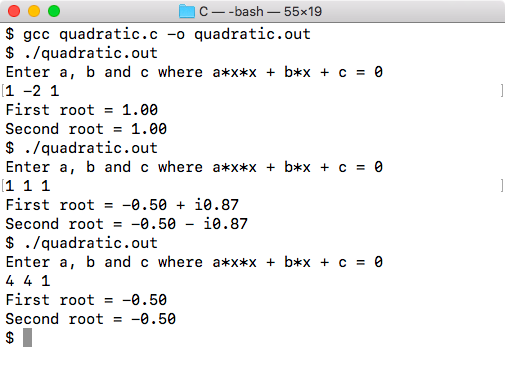
C program to find roots of a quadratic equation: Coefficients of the equation are assumed to be integers, but roots may or may not be real (imaginary).
For a quadratic equation ax2+ bx + c = 0 (a≠0), discriminant (b2-4ac) decides the nature of roots. If it's less than Zero, the roots are imaginary. If it's greater than Zero, the roots are real. If it's Zero, the roots are equal. To calculate the square root of the discriminant, we use sqrt function of the "math.h" header file.
For a quadratic equation, the sum of its roots = -b/a and the product of its roots = c/a. Let's look at the program now.
Roots of a Quadratic equation in C
#include <math.h>
int main()
{
int a, b, c, d;
double root1, root2;
printf("Enter a, b and c where a*x*x + b*x + c = 0\n");
scanf("%d%d%d", &a, &b, &c);
d = b*b - 4*a*c;
if (d < 0) { // complex roots, i is for iota (√-1, square root of -1), %lf for double data-type
printf("First root = %.2lf + i%.2lf\n", -b/(double)(2*a), sqrt(-d)/(2*a));
printf("Second root = %.2lf - i%.2lf\n", -b/(double)(2*a), sqrt(-d)/(2*a));
}
else { // real roots
root1 = (-b + sqrt(d))/(2*a);
root2 = (-b - sqrt(d))/(2*a);
printf("First root = %.2lf\n", root1);
printf("Second root = %.2lf\n", root2);
}
return 0;
}