Java program to multiply two matrices, before multiplication, we check whether they can be multiplied or not. We use the simplest method of multiplication. There are more efficient algorithms available. Also, this approach isn't efficient for sparse matrices, which contains a large number of elements as zero.
Java matrix multiplication
class MatrixMultiplication
{
public static void main(String args[])
{
int m, n, p, q, sum = 0, c, d, k;
Scanner in = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of first matrix");
m = in.nextInt();
n = in.nextInt();
int first[][] = new int[m][n];
System.out.println("Enter elements of first matrix");
for (c = 0; c < m; c++)
for (d = 0; d < n; d++)
first[c][d] = in.nextInt();
System.out.println("Enter the number of rows and columns of second matrix");
p = in.nextInt();
q = in.nextInt();
if (n != p)
System.out.println("The matrices can't be multiplied with each other.");
else
{
int second[][] = new int[p][q];
int multiply[][] = new int[m][q];
System.out.println("Enter elements of second matrix");
for (c = 0; c < p; c++)
for (d = 0; d < q; d++)
second[c][d] = in.nextInt();
for (c = 0; c < m; c++) {
for (d = 0; d < q; d++) {
for (k = 0; k < p; k++)
sum = sum + first[c][k]*second[k][d];
multiply[c][d] = sum;
sum = 0;
}
}
System.out.println("Product of the matrices:");
for (c = 0; c < m; c++) {
for (d = 0; d < q; d++)
System.out.print(multiply[c][d]+"\t");
System.out.print("\n");
}
}
}
}
Output of program: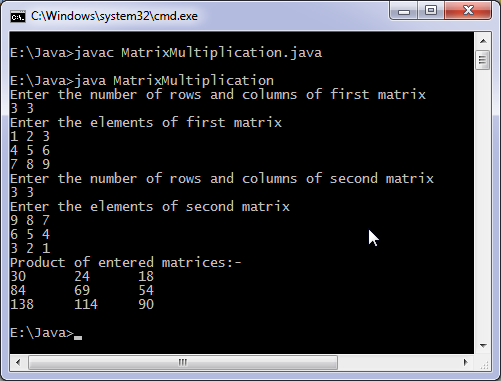
Download Matrix multiplication program class file.